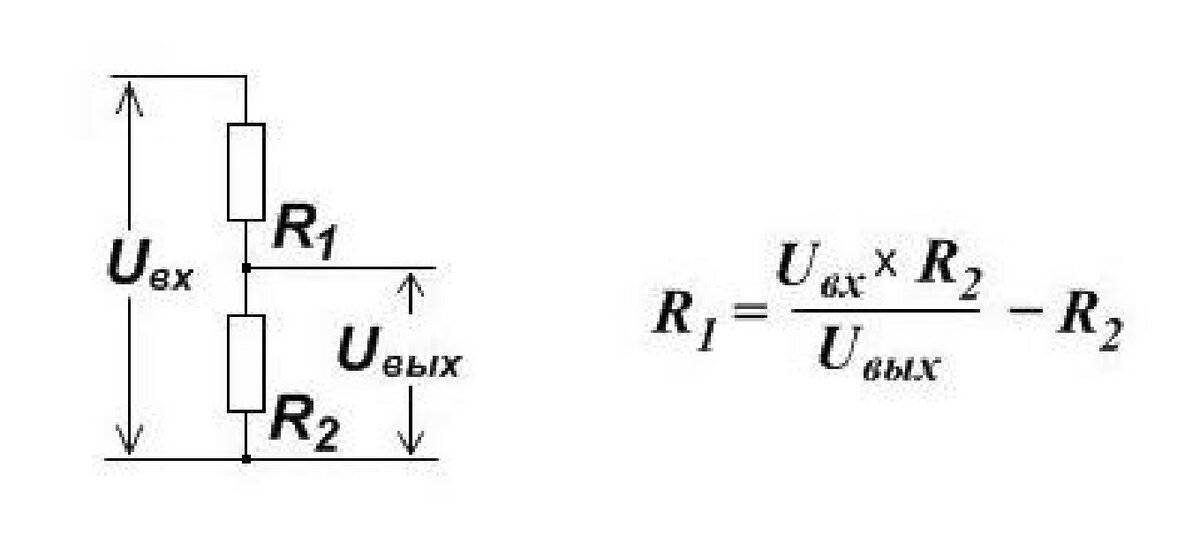Онлайн калькулятор расчета делителя напряжения

Ограничения в применении

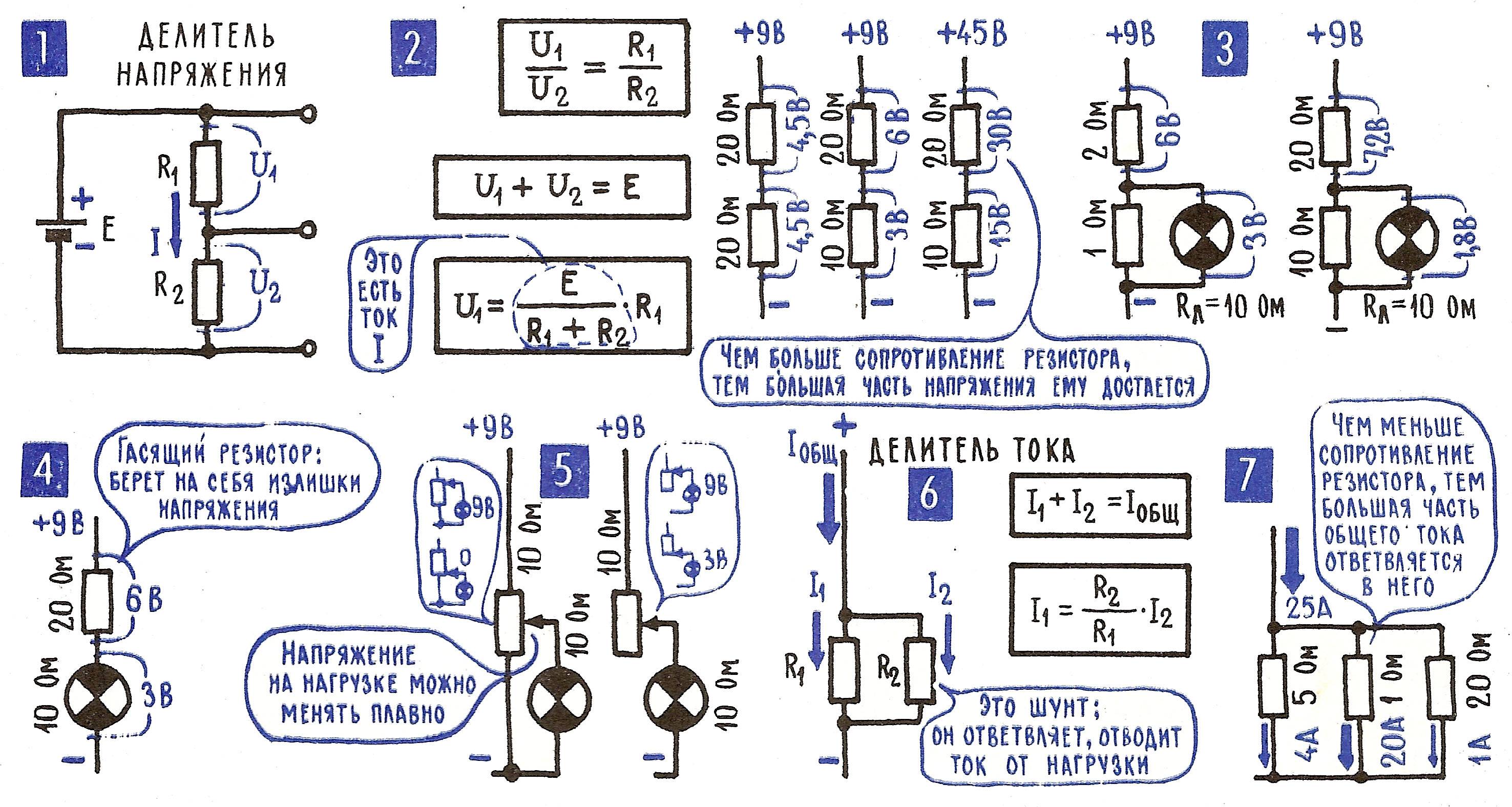
Из приведенных в таблице примеров расчетов хорошо видно, как значительно увеличиваются потери при уменьшении сопротивления цепи. Энергия расходуется впустую для нагрева окружающей среды. При большой мощности рассеивания приходится использовать принудительные системы охлаждения, пассивные радиаторы.

В приведенных расчетах не учитывалась нагрузка. Если добавить соответствующее реальным условиям сопротивление, образуются дополнительные потери в параллельной цепи.

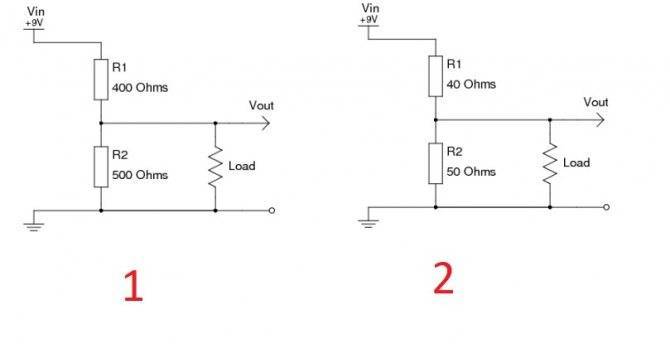Влияние сопротивления нагрузки

На первой части рисунка изображен типовой делитель, обеспечивающий выходное напряжение 5 V. При потреблении тока 0,01 А сопротивление нагрузки составит 0,5 кОм. Пользуясь формулой расчета для параллельной цепи, несложно выяснить суммарное значение R = 1/(1/R2 + 1/Rнагрузки) = 0,25 кОм. Это добавление уменьшит плановое значение Uвых до 3,46 V.

Уменьшением R2 можно снизить вредное влияние на выходное напряжение (4,75 V). Однако такой способ, приведенный на второй части рисунка, сопровождается значительными потерями энергии. Ток будет проходить по участку с меньшим сопротивлением, не выполняя полезные функции. В данном примере необходимо выбрать R1, рассчитанный на мощность не менее 2 Вт, чтобы обеспечить надежную работу устройства.

Чему равно напряжение.

Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.

Изображение вольтметра и электрической цепи

Напряжение обозначается латинской , а измеряется в . Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.

Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении

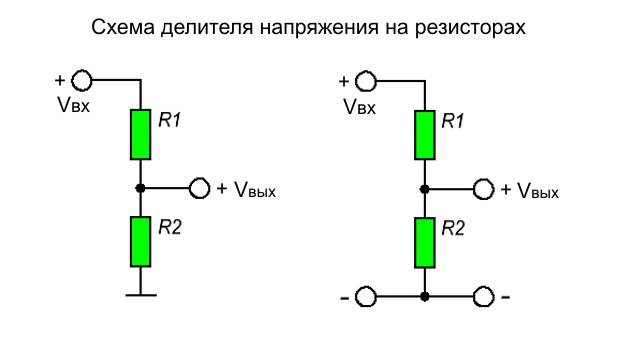
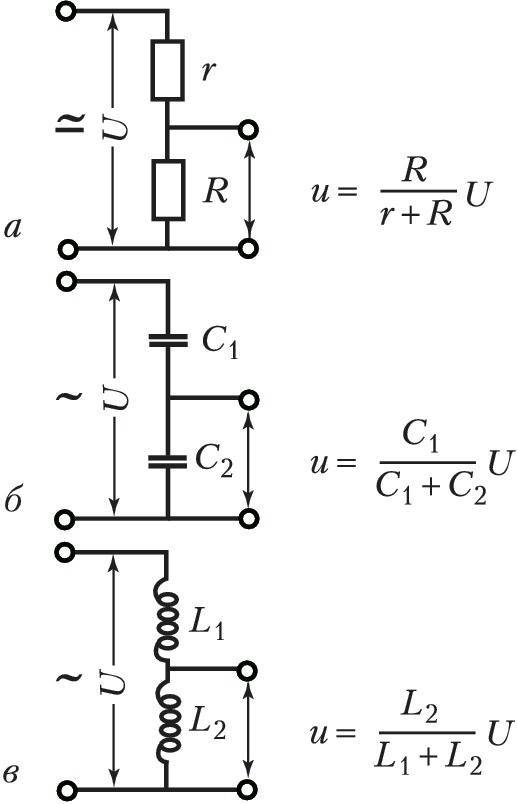
Делители напряжения на резисторах

Делители напряжения могут применяться как в цепях постоянного тока, так и в цепях тока переменного. Делители напряжения на резисторах подходят и для тех, и для других цепей, однако используются они только в цепях низкого напряжения. Для питания устройств делители напряжения на резисторах не применяют.
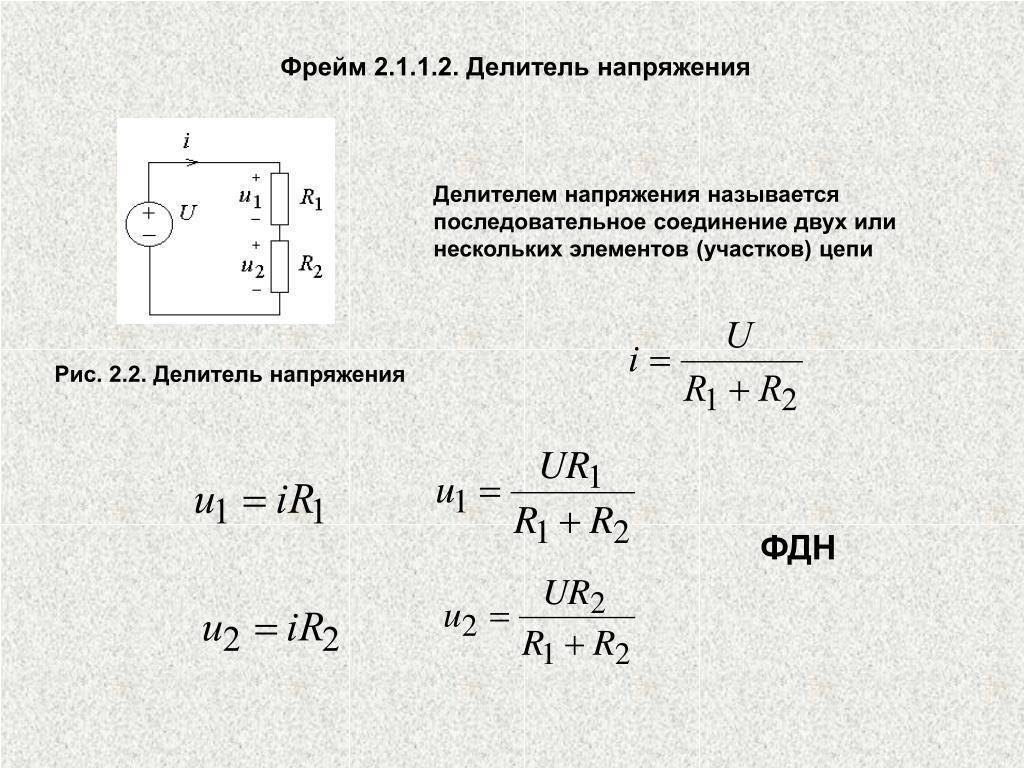
В простейшем виде резистивный делитель напряжения состоит всего из пары резисторов,

соединенных последовательно. Делимое напряжение подается на делитель, в результате на каждом резисторе падает определенная доля этого напряжения, пропорциональная номиналу резистора. Сумма падений напряжений равна здесь напряжению подаваемому на делитель.
Согласно закону Ома для участка электрической цепи, на каждом резисторе падение напряжения будет прямо пропорционально току и величине сопротивления резистора. А согласно первому правилу Кирхгофа, ток через данную цепь будет везде один и тот же

Так, на каждый резистор придутся падения напряжения:

И напряжение на концах участка цепи будет равно:

А ток в цепи делителя составит:

Теперь если подставить выражение для тока в формулы для падений напряжений на резисторах, то получим формулы для нахождения величин напряжений на каждом из резисторов делителя:

Используя делитель напряжения на резисторах для тех или иных целей, важно понимать, что присоединенная к одному из плеч делителя нагрузка, будь то измерительный прибор или что-нибудь другое, должна иметь собственное сопротивление значительно большее (в 10-100 раз), чем общее сопротивление резисторов, образующих делитель. Так, чтобы в расчетах этим сопротивлением, включенным параллельно R2, можно было бы пренебречь.Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке (см. выше, в предыдущем абзаце)

Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R = R1+R2. Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко требуемому отношению напряжений, а сумма величин близка расчетной. 

выше, в предыдущем абзаце). Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R = R1+R2. Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко требуемому отношению напряжений, а сумма величин близка расчетной. 

Расчёт делителя напряжения, состоящего из более чем трех резисторов можно по специальным формулам. Существуют методики, позволяющие выводить формулы для схем, содержащих от четырех и более резисторов.

Виды и принцип действия

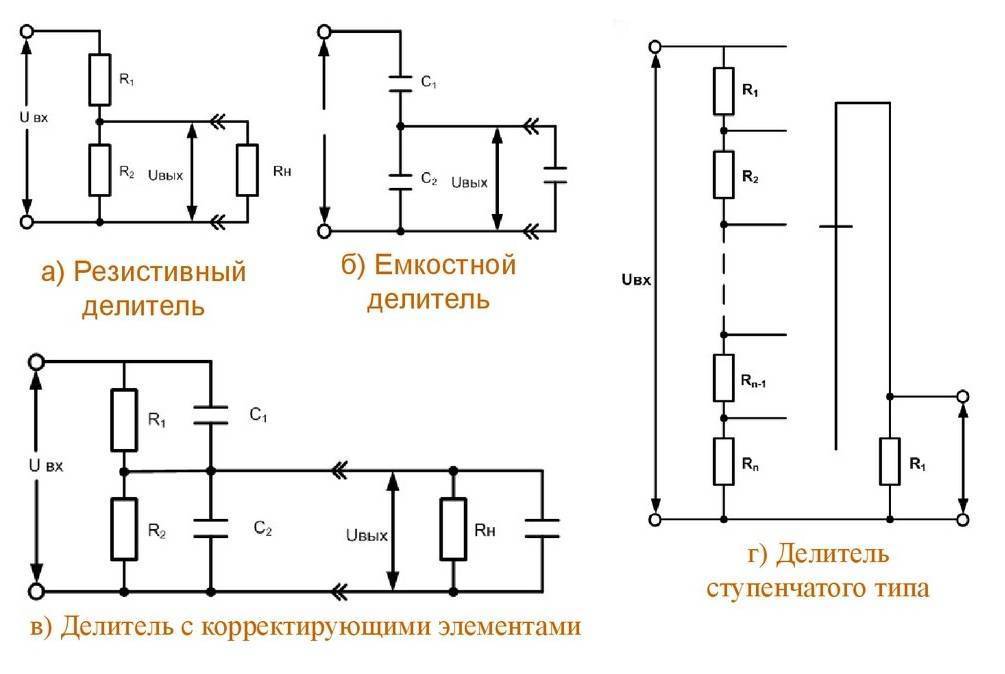
В данной публикации подробно рассмотрен резистивный делитель напряжения. Подразумевается линейность характеристики цепи. В таких схемах упрощен расчет сопротивления для понижения напряжения до необходимого уровня. При подключении источника постоянного тока происходит деление напряжений прямо пропорционально значениям электрических сопротивлений нижнего и верхнего плеча.

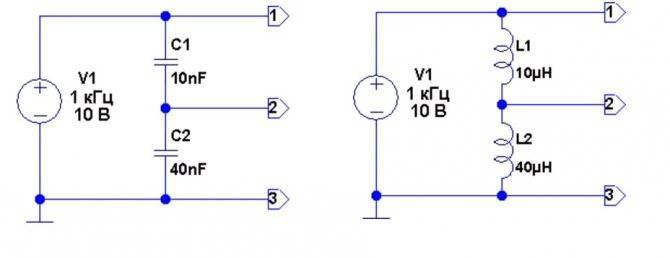Цепи с реактивными характеристиками

Что такое электрическое сопротивление

Если составить аналогичную схему с конденсаторами, то на вход для поддержания нормальной функциональности придется подать синусоиду. В этом случае также будет выполнено распределение напряжений на элементах с емкостными характеристиками. Однако этот процесс надо рассматривать в динамике, с учетом частоты и соответствующего изменения амплитуды. Аналогичную методику применяют при работе с индуктивными компонентами.

Значения реактивных сопротивлений:

• Rc=1/(2*f*π*C);
• RL=2*f*π*C.

По формулам видно, что сопротивление конденсатора/ катушки обратно (прямо) пропорционально емкости/ индуктивности. Соответственно выбирают значения элементов для деления напряжения.

В представленных примерах принимают бесконечно большим внутреннее сопротивление нагрузки. Для реальных расчетов пользуются более сложными формулами с поправочными коэффициентами. Учитывают действительные комплексные характеристики цепей.

К сведению. В стабилизаторах напряжения и некоторых иных устройствах сопротивление плеча делителя обладает нелинейными параметрами.

Калькулятор делителя напряжения

Разделитель напряжения представляет собой схему, используемую для создания напряжения, которое меньше или равно входному напряжению.

Как найти выходное напряжение цепи делителя

Два делителя напряжения резистора являются одной из наиболее распространенных и полезных схем, используемых инженерами. Основная цель этой схемы заключается в уменьшении входного напряжения до более низкого значения в зависимости от отношения двух резисторов. Этот калькулятор помогает определить выходное напряжение схемы делителя с учетом входного (или источника) напряжения и значений резисторов

Обратите внимание на то, что выходное напряжение в реальных схемах может быть различным, поскольку резистор и сопротивление нагрузки (при подключении выходного напряжения) становятся факторами

Уравнение

$$ V_ $$ = Выходное напряжение. Это уменьшенное напряжение.

$$ V_ $$ = Входное напряжение.

$$ R_ $$ и $$ R_ $$ = значения резистора. Отношение $$ frac > + R_ > $$ определяет масштабный коэффициент.

Приложения

Поскольку делители напряжения довольно распространены, их можно найти в ряде приложений. Ниже приведены лишь некоторые из мест, где эта схема найдена.

потенциометры

Возможно, наиболее распространенной схемой делителя напряжения является то, что используется потенциометр, который является переменным резистором. Схематическое изображение потенциометра показано ниже:

«Горшок» обычно имеет три внешних контакта: два являются концами резистора, а один подключен к рычагу стеклоочистителя. Стеклоочиститель разрезает резистор пополам и перемещает его, регулируя соотношение между верхней половиной и нижней половиной резистора. Соедините два внешних выводы к напряжению (вход) и ссылку (земля) со средним (стеклоочистители штифтом) в качестве выходного контакта и вы сам делитель напряжения.

Уровневые сдвиги

Другая область, в которой используются делители напряжения, – это когда напряжение должно быть выровнено. Наиболее распространенным сценарием является взаимодействие сигналов между датчиком и микроконтроллером с двумя разными уровнями напряжения. Большинство микроконтроллеров работают при напряжении 5 В, в то время как некоторые датчики могут принимать только максимальное напряжение 3, 3 В. Естественно, вы хотите выровнять напряжение от микроконтроллера, чтобы избежать повреждения датчика. Пример схемы показан ниже:

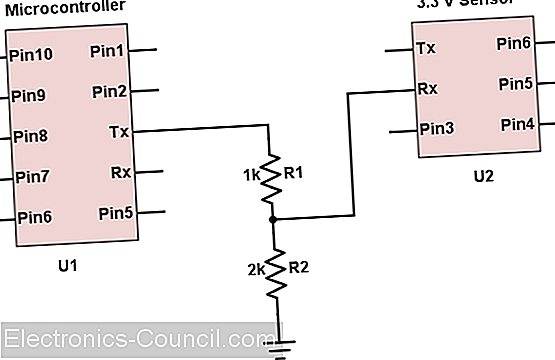
Схема выше показывает схему делителя напряжения, включающую резистор 2 кОм и 1 кОм. Если напряжение от микроконтроллера составляет 5 В, то пониженное напряжение на датчик рассчитывается как:

Этот уровень напряжения теперь безопасен для работы датчика

Обратите внимание, что эта схема работает только для выравнивания напряжений и не выравнивания

Ниже приведены некоторые другие комбинации резисторов, используемые для выравнивания часто встречающихся напряжений:

Комбинация резисторов	использование
4, 7 кОм и 6, 8 кОм	От 12 В до 5 В
4, 7 кОм и 3, 9 кОм	9V до 5V
3, 6 кОм и 9, 1 кОм	От 12 В до 3, 3 В
3, 3 кОм и 5, 7 кОм	От 9 В до 3, 3 В

Чтение резистивного датчика

Многие датчики являются резистивными устройствами и большинством микроконтроллеров считывают напряжение, а не сопротивление. Таким образом, резистивный датчик обычно подключается в цепи делителя напряжения с резистором для взаимодействия с микроконтроллером. Пример установки показан ниже:

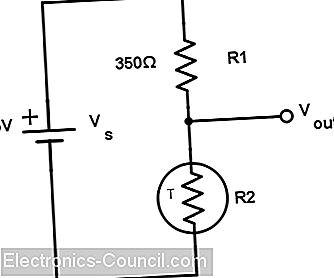
Термистор – это датчик, сопротивление которого изменяется пропорционально температуре. Скажем, что термистор имеет сопротивление комнатной температуре 350 Ом. Сопряженное сопротивление выбирается равным 350 Ом.

Когда термистор находится при комнатной температуре, выходное напряжение:

Когда температура увеличивается, сопротивление термистора изменяется до 350, 03 Ом, выход изменяется на:

Такое небольшое изменение напряжения обнаруживается микроконтроллером. Если функция передачи термистора известна, теперь можно рассчитать эквивалентную температуру.

Дальнейшее чтение

Техническая статья – Разделители напряжения и тока: что это такое и что они делают

Учебник – Глава 6 – Цепи Divider и законы Кирхгофа

Учебник – Потенциометр в качестве делителя напряжения

Как понизить напряжение с помощью резистора

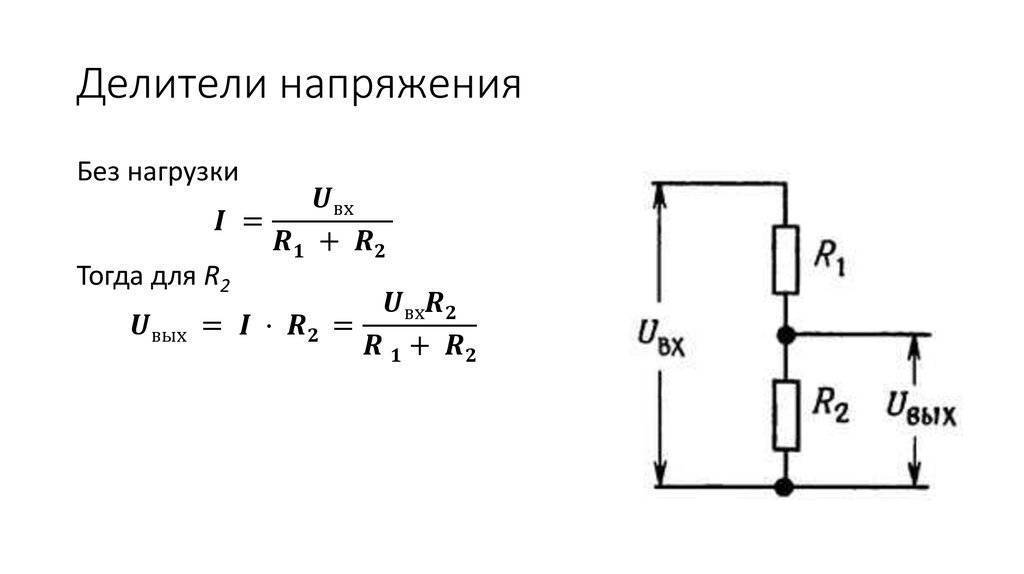
Чтобы нагрузка, которую требуется запитать, не сгорела, часто возникает необходимость снизить входное напряжение. Проще всего этого можно добиться, используя схему с двумя резисторами, более известную как делитель напряжения. Классическая схема выглядит так:

В этом случае напряжение подаётся на два резистора с использованием параллельного подключени, а на выходе его получают с одного. Подбор номиналов резисторов осуществляют по формуле так, чтобы напряжение, снимаемое на выходе, составляло какую-то часть от подаваемого. Расчет резистора для понижения напряжения можно воспользовавшись формулой, основанной на законе Ома:

Uвых= (Uвх*R2)/(R1+R2), где

Uвх – напряжение на входе, В;

Uвых – напряжение на выходе, В

R1 – показатель сопр. 1-ого резистора (Ом)

R2 – показатель сопр. 2-ого элемента, (Ом)

Подбор резистора для понижения напряжения

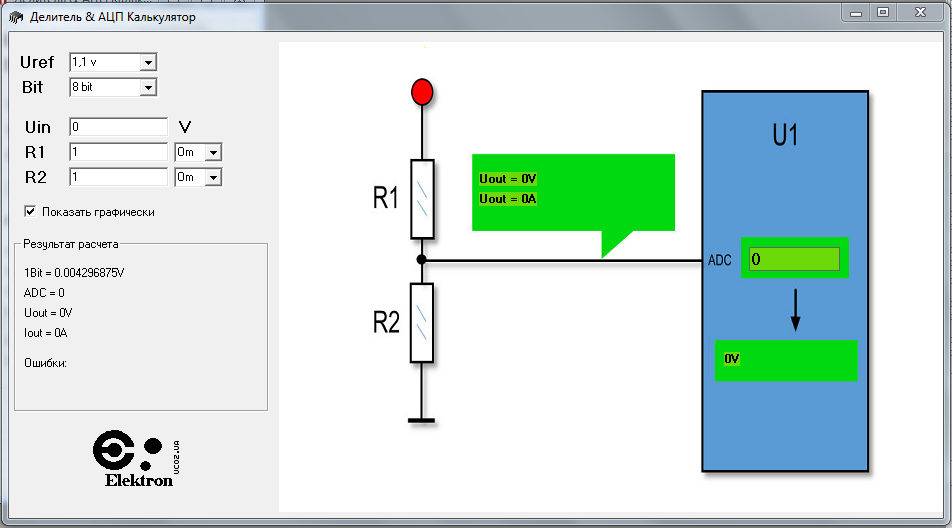
Для подбора нужного сопротивления резистора можно воспользоваться готовыми онлайн-калькуляторами или программами для моделирования работы электронных схем. Симуляторы электрических цепей способны не только рассчитать напряжение на выходе в зависимости от сопротивления элементов и способа их подключения, но и обладают функционалом, позволяющим визуализировать то, как падает ток и напряжение на резисторе. Например, приложение EveryCircuit позволяет изменять в схеме параметры элементов, выбирать скорость симуляции, получать данные в различных точках. При этом можно наблюдать за динамикой изменения значений, используя для ввода входных параметров вращающийся лимб в нижнем правом углу.

Существует ещё ряд бесплатных программ для эмуляции, позволяющие выполнить, в том числе, расчёт резистора при понижении напряжения, например:

• EasyEDA;
• Circuit Sims;
• DcAcLab;

и другие.

В статье мы ознакомились с понятием сопротивления, узнали о его единицах измерения, о маркировке резисторов, о программах эмулирующих работу цепи и облегчающих подбор нужного сопротивления, а также рассмотрели примеры расчёта падения напряжения на резисторе.

Параллельное и последовательное соединение резисторов, решение задач

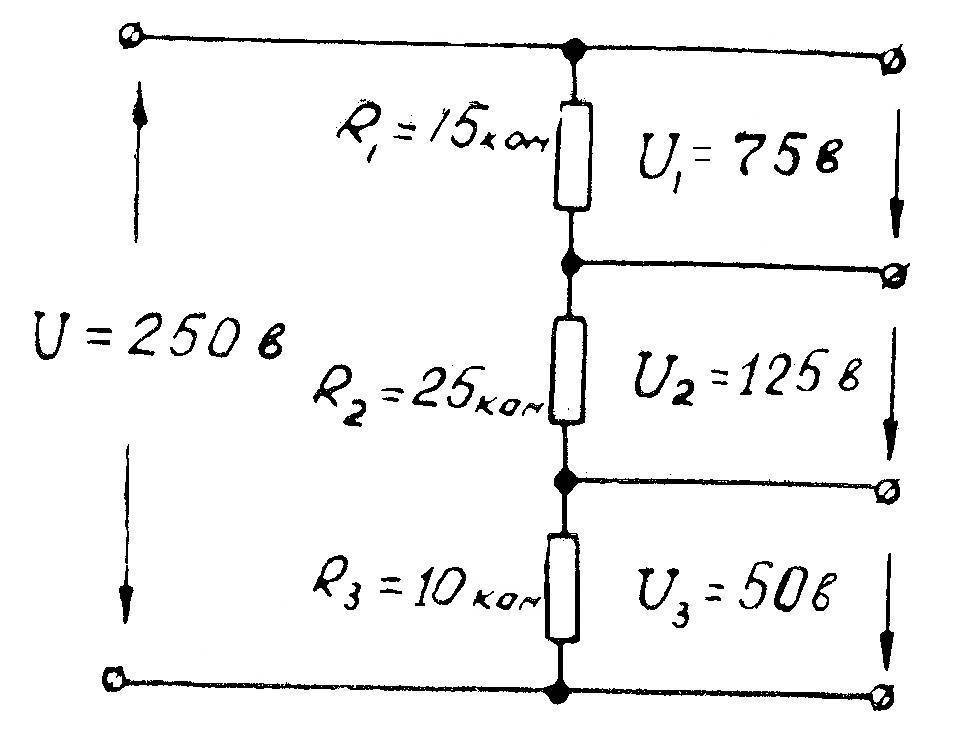
Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно. Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. На схеме присутствует параллельная и последовательная часть соединения элементов

Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?. Будет интересно Как прочитать обозначение (маркировку) резисторов

Будет интересно Как прочитать обозначение (маркировку) резисторов

Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.

Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.

Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше. Теперь образовалась ситуация — включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом

Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех. Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще

Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом

В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.

Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно. На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.

Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

• Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
• Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.

Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Типы подключений.

Применение

Использование такой схемотехники на практике демонстрируют следующие примеры. Для расчетов электрических параметров без учета сопротивления нагрузки подойдут рассмотренные выше ручные и автоматизированные методики.

Потенциометры

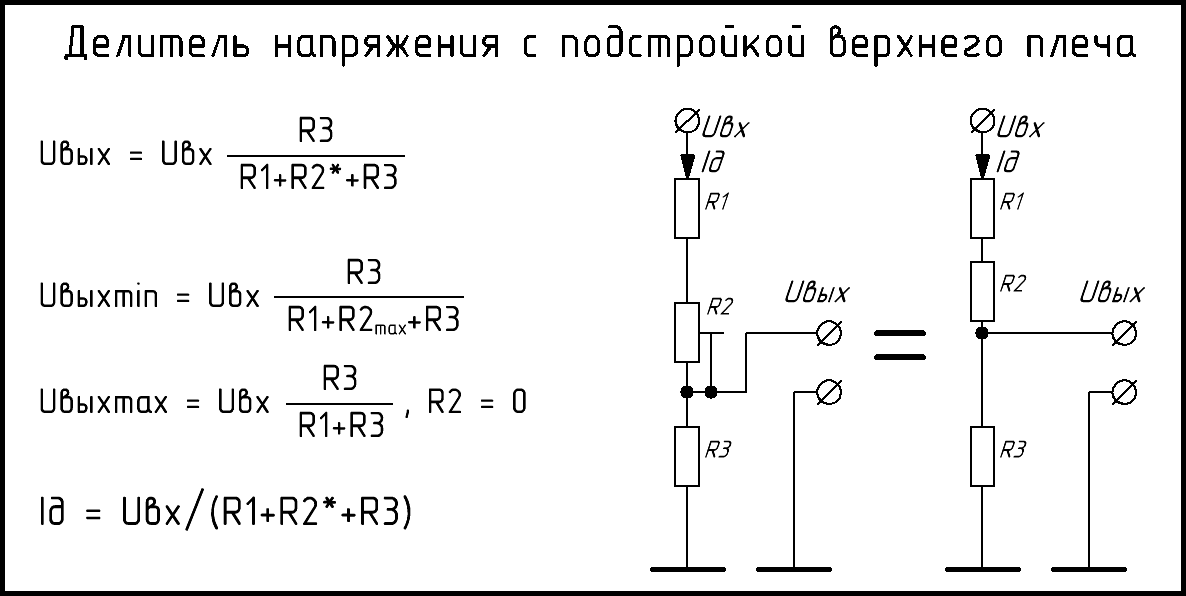
Если резистор оснастить ползунком и соответствующим приводом, сопротивления можно будет менять плавно. Это решение позволяет точнее менять напряжения на выходе, по сравнению с дискретными схемами. Главный недостаток – усложнение конструкции, что, кроме удорожания, снижает надежность. Приходится обеспечивать герметичность рабочей зоны для исключения загрязнения и предотвращения коррозийных процессов.

Принципиальная схема потенциометра

Резистивные датчики

В этом варианте пользуются способностью некоторых материалов увеличивать/ уменьшать электрическое сопротивление под воздействием температуры, светового потока, других внешних воздействий. Созданный на основе этих принципов датчик устанавливают в плечо делителя. По уровню напряжения на выходе контролируют изменение соответствующих параметров.

Цепи обратной связи в усилителях

Таким решением обеспечивают необходимый коэффициент усиления. На представленной ниже схеме этот параметр не будет никогда ниже единицы. Для повышения уровня преобразования увеличивают значение сопротивления R2 по отношению к R1.

Делитель напряжения в цепи обратной связи

Простейшие электрические фильтры

Для фильтрации заменяют конденсатором резисторы R1 или R2. В первом варианте устройство беспрепятственно пропускает высокочастотные составляющие. При снижении частоты до определенного уровня реактивное сопротивление увеличивается, препятствует прохождению тока. Аналогичным образом делают изменения в нижнем плече делителя с целью отсечения низких частот.

Усилитель напряжения

Переменным резистором изменяют уровень сигнала для получения необходимой громкости звучания. В таких устройствах применяют элементы с логарифмической характеристикой изменения сопротивления, что хорошо соответствует естественному механизму восприятия человеческими органами слуха.

Параметрический стабилизатор напряжения

В таких схемах нижнее плечо делителя можно создать с применением стабилитрона. Его вольтамперные характеристики выбирают таким образом, чтобы выходное напряжение сохраняло нужное значение при изменении входных параметров.

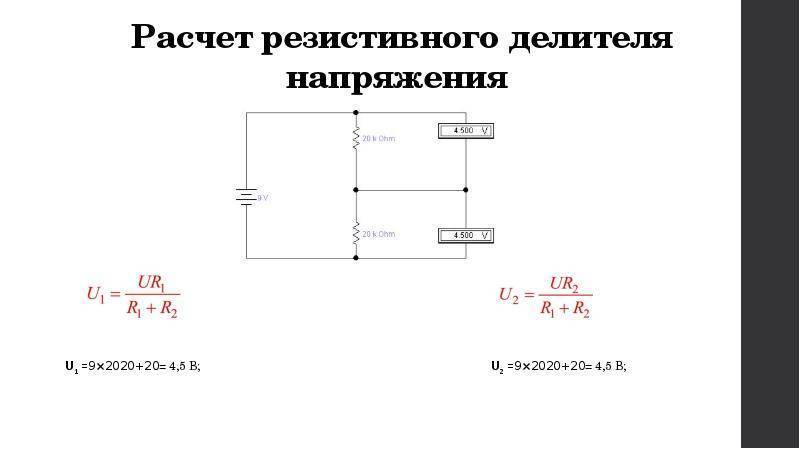
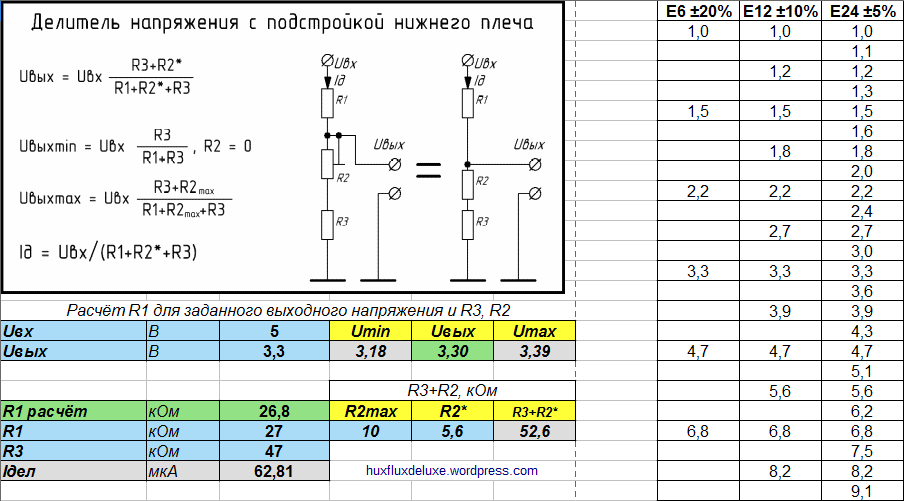
Расчет делителя напряжения на резисторах.

Использование делителя напряжения на резисторах очень неэкономичный, затратный способ понижения величины напряжения, так как неиспользуемая энергия рассеивается на сопротивлении (превращается в тепловую энергию). КПД очень низкий. Но несмотря на это в схемах системных плат ноутбуков очень часто можно встретить делители напряжения на резисторах. Обычно применяются в схемах заряда и других преобразователях в измерительных целях и в качестве формирования управляющих сигналов.

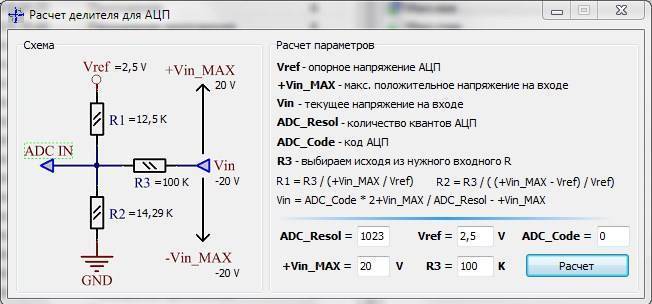
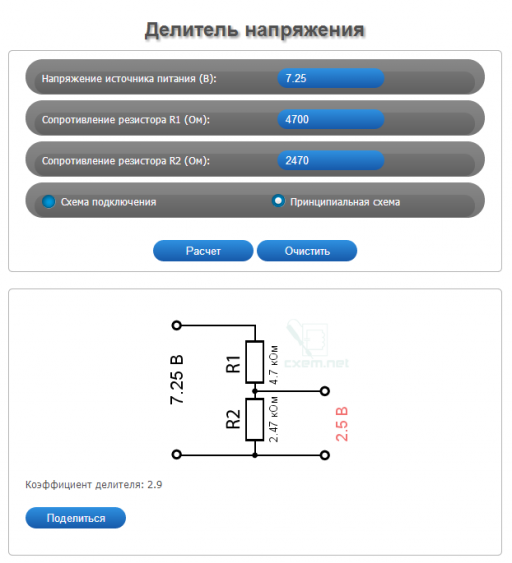
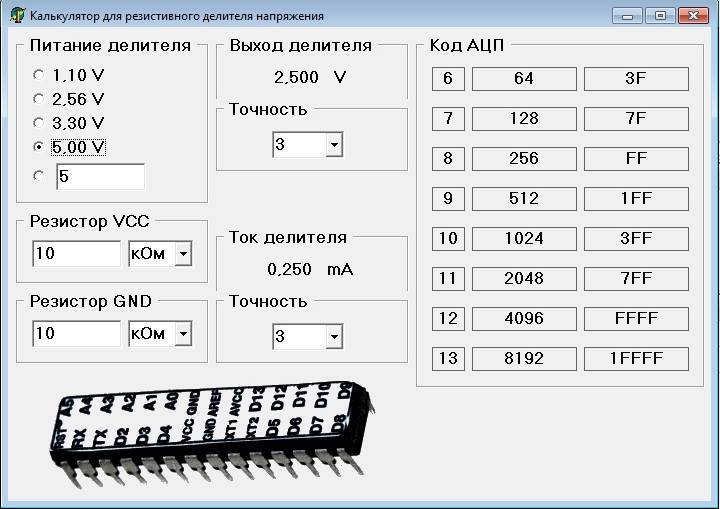
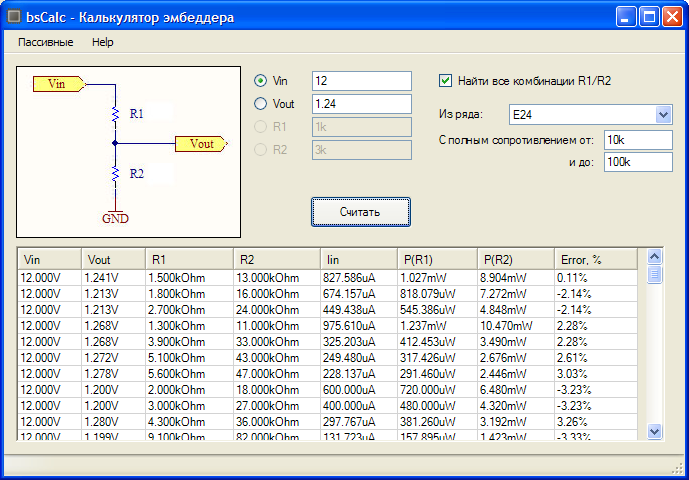
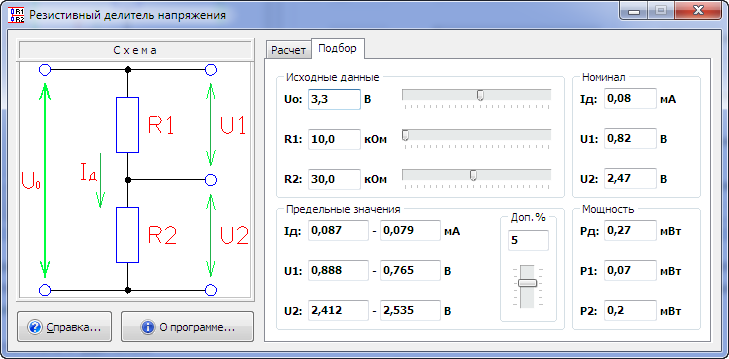
Часто сталкиваешься с расчетами делителей в случае повреждения плат коррозией. Работаешь с формулами, переключаешься с одного дела на другое. Вместо паяльника берешь в руки бумагу, листок и считаешь… Для ускорения своей работы и так сказать — автоматизации. Ниже приведены 3 онлайн калькулятора расчета делителя напряжения на резисторах. На просторах интернета можно сказать что их много, я соглашусь, но они в основном направлены для расчета выходного напряжения. Уникальность моих калькуляторов заключается в том что мы можем высчитать номинал утраченных R1 или R2, а таких в сети к сожалению пока не встретил. И поэтому решил сам их создать, для своей работы и возможно для вашей.

В каждом из калькуляторов изъято одно из значений, ведь всякое бывает… Бывает что нужно узнать выходное напряжение или утрачены номиналы одного из резисторов делителя.

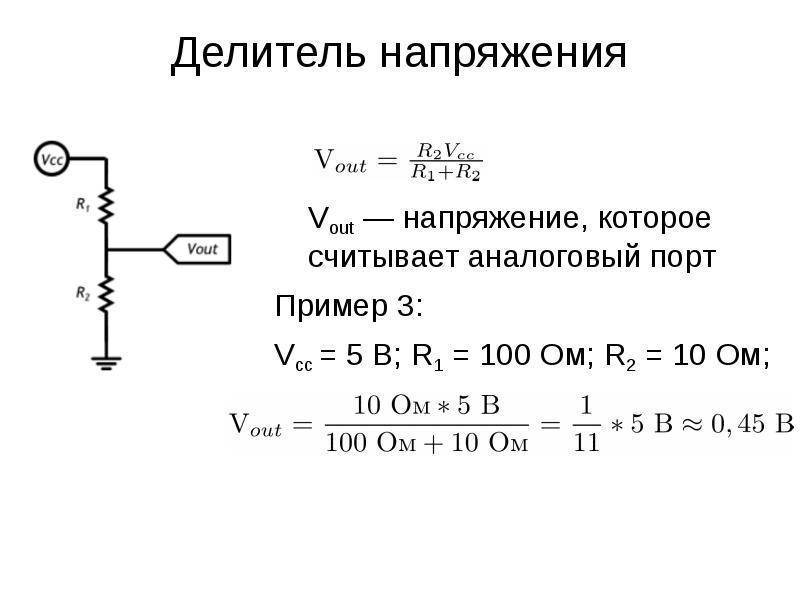
Начнем с расчета, если нам известны три величины из приведенной схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Расчет выходного напряжения с делителя, если известны R1, R2 и U(входное).

Формула расчета:

(U(вх)*R2)/(R1+R2)=U(вых)

Далее расчет сопротивления R1, с известными R2, U(входное) и U(выходное).

Расчет сопротивления R1 делителя, если известны R2, U(входное) и U(выходное).
	Формула расчета: (U(вх)*R2)/U(вых)=R1

И расчет сопротивления R2, с известными R1, U(входное) и U(выходное).

Расчет сопротивления R2 делителя, если известны R1, U(входное) и U(выходное).

Формула расчета:

(R1*U(вых))/(U(вх)-U(вых))=R2

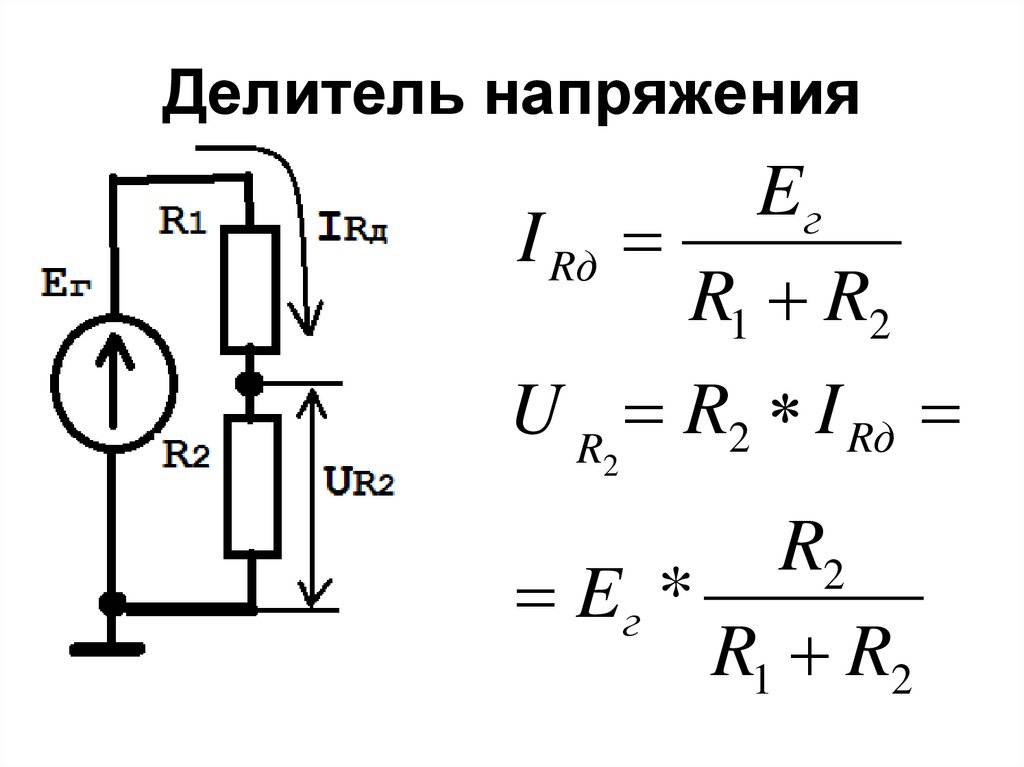
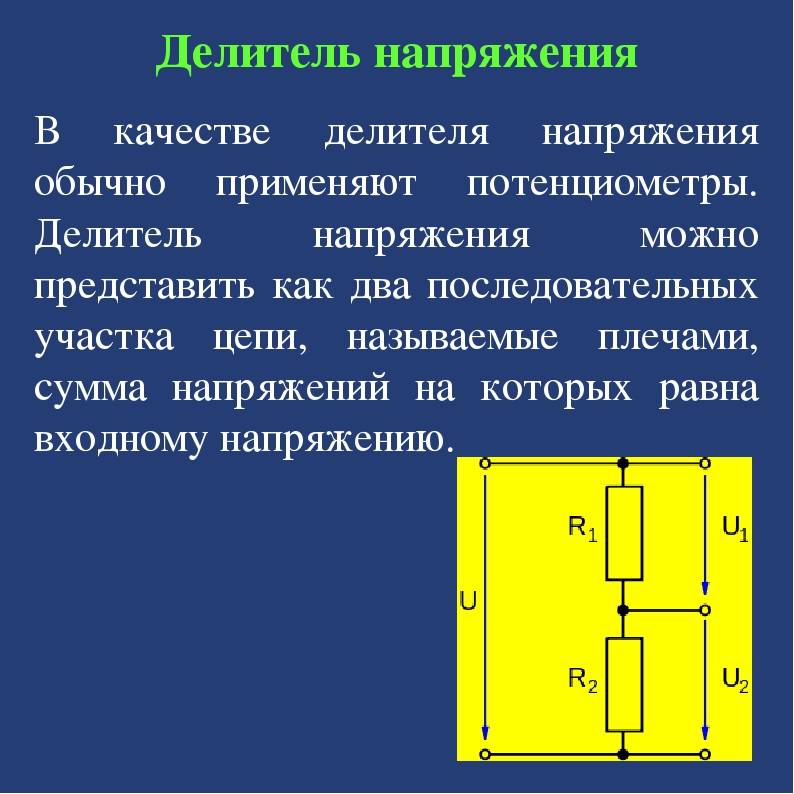
Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Емкостной делитель напряжения

Простейший емкостной делитель напряжения состоит из двух последовательно соединенных конденсаторов и используется для снижения величины U на отдельных элементах электрической цепи.

Делитель постоянного напряжения на конденсаторах чаще всего применяют многоуровневых инверторов напряжения, широко используемых как на электроподвижном составе, так и в других направлениях силовой электроники.

Главная сложность практического применения такой схемы (и всех подобных схем) заключается в невозможности обеспечения равномерного разряда конденсаторов, вследствие чего напряжения на них будет распределяться не поровну. Чем сильнее разряжен один конденсатор по сравнению с другим (иди с другими), тем большая разница в U будет на них, что наглядно отображает формула:

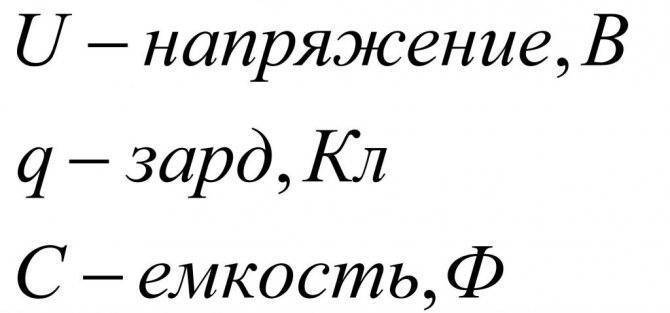
По этой причине подобные схемы крайне нестабильно работают и обязательно предусматривают узлов подзарядки конденсаторов с целью выравнивания напряжения на последних.

Емкостной делитель напряжения в цепи переменного тока

В радиоэлектронике в большей степени находят применение емкостные делители переменного напряжения.

Конденсатор, как и катушка индуктивности, относится к реактивному элементу, то есть потребляет реактивную мощность от источника переменного тока, в отличие от резистора, который является активным элементов и потребляет исключительно активную мощность.

Реактивный элемент

Здесь следует кратко пояснить разницу между активной и реактивной мощностями. Активная мощность выполняет полезную работу и реализуется только в том случае, когда ток и напряжение направлены в одном направлении и не отстают друг от друга, то есть находятся в одной фазе, что имеет место только на резисторе. На конденсаторе ток отстает от напряжения на угол φ = 90°. В результате чего ток напряжение находятся в противофазе, поэтому когда ток имеет максимальное значение напряжение равно нулю, а произведение этих двух величин дают мощность, которая в таком случае равна нулю, так как один из множителей равен нулю. Следовательно, мощность не потребляется.

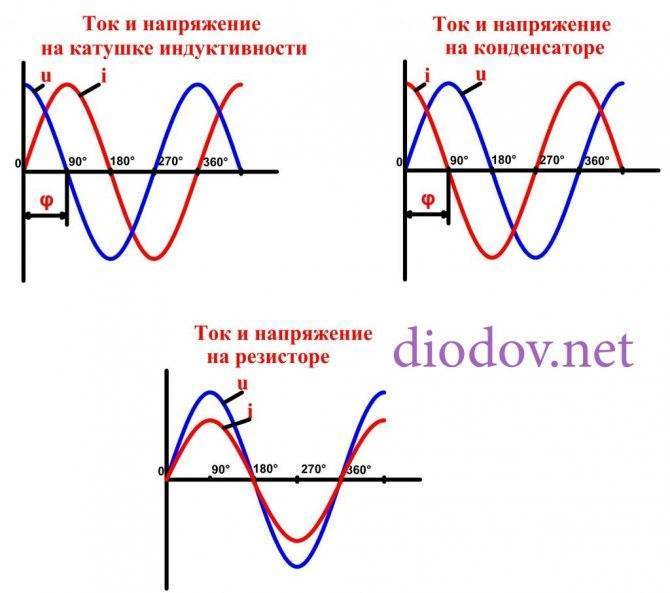
Аналогичные процессы протекают и в цепи с катушкой индуктивности. Разница лишь в том, что на индуктивности i отстает от u на угол φ = 90°.

Реактивная мощность проявляется только в цепях переменного тока. Она составляет часть полной мощности и определяется по формуле:

Реактивная мощность в отличие от активной, не потребляется нагрузкой, а циркулирует между источником питания и нагрузкой. Поэтому конденсатора и катушка индуктивности являются реактивными элементами, не потребляющими активную мощность и по этой причине они практически не нагреваются.

Расчет сопротивления делителя напряжения на конденсаторах заключается в определении необходимых значений сопротивлений.

Сопротивление конденсатора XC является величиной не постоянной и зависит от частоты переменного тока f и емкости C:

Как видно из формулы, сопротивление снижается с увеличением частоты и емкости. Для постоянного тока, частота которого равна нулю, сопротивление стремится к бесконечности, поэтому, рассматриваемая далее схема емкостного делителя напряжения не применяется постоянном токе.

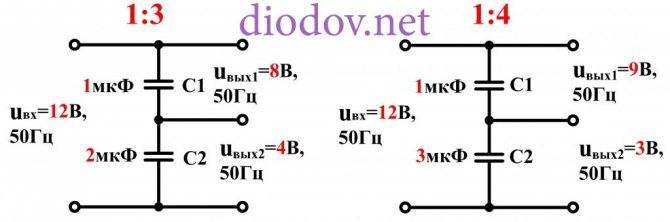
Для снижения величины uвых, например в два раза, емкости C1 и C2 должны быть равны. Универсальные формулами для определения выходных uвых1 и uвых2 в зависимости от входного и емкостей C1 и C2 имеют вид, аналогичный для резисторных делителей:

Поскольку частота переменного тока для всех конденсаторов одинакова, то формулу можно упростить:

Индуктивный делитель напряжения

В качестве делителей переменного напряжения также, но гораздо реже, применяют катушки индуктивности, которые относятся к реактивным элементам. Однако, в отличие от конденсаторов, которые являются накопителями электрического поля, катушки индуктивности накапливают магнитное поле.

Индуктивное сопротивление зависит от индуктивности L и частоты переменного тока f. С ростом этих параметров сопротивление катушки переменному току возрастает.

XL = 2πfL.

Упрощенный вариант формулы:

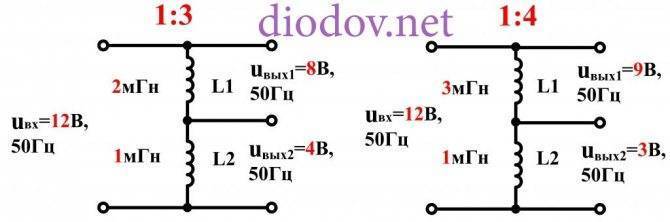
Как вы наверняка уже заметили, чтобы рассчитать емкостной делитель напряжения достаточно знать емкости конденсаторов, а индуктивный делитель – индуктивности.

• Делитель напряжения на резисторах
• Инвертор напряжения
• Умножитель напряжения
• Замена электролитического конденсатора

Расчет делителя напряжения на резисторах

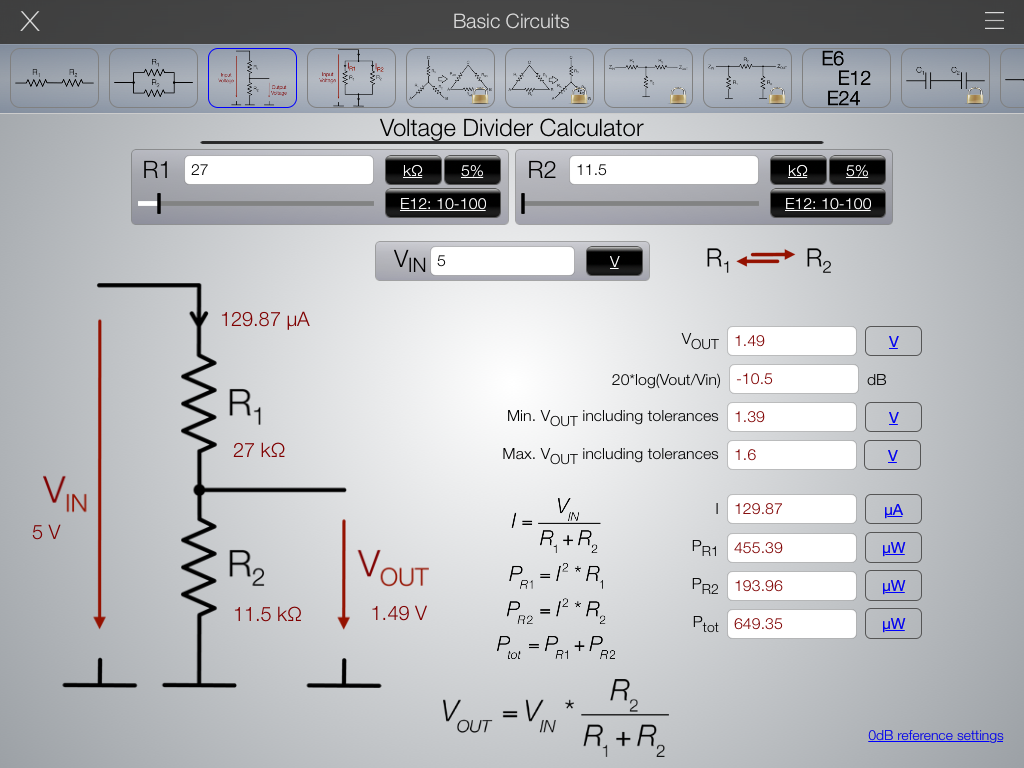
Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

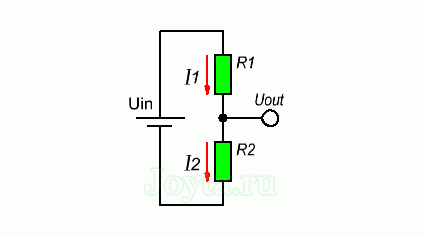
Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Тестер транзисторов / ESR-метр / генератор

Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…

Подробнее

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом виде: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.